Options volatility
Volatility is an important concept in the context of option trading, but it’s also one of the more complex ones to understand. In financial markets, volatility captures the amount of fluctuation in asset prices and is generally calculated as the annualized standard deviation of daily price changes, normally expressed as a percentage. To convert the annual level of volatility to the daily volatility, the annualized number is divided by the square root of 252 (~16), as there are 252 trading days in a year. An annualized volatility of 16% therefore translates to a daily volatility of 1%, meaning that on a daily basis the price moves on average 1%. It should also be noted that volatility only says something about the degree of price fluctuation, not whether the change is up or down.
There are two types of volatility:
- Historical volatility, also called realized volatility, is the backward-looking measure of volatility. It measures the level of price fluctuations in the past by looking at the historical price movement.
- Implied volatility is the forward-looking measure of volatility. In the case of options, the implied volatility is ‘implied’ from their price and reflects the market’s expectation of the volatility of the option’s underlying asset from now until the expiration of the option.
Implied volatility is one of the inputs used in option pricing models, e.g. the Black-Scholes model, along with the price of the underlying asset, the option’s strike price, its expiration date, the interest rate and dividends. Most of these inputs can be readily observed in the market, but the implied volatility can’t. Using the market price of the option, it is possible to reverse engineer an option pricing model to find out what level of implied volatility is priced in. The other exception is the dividend, which in normal conditions can be determined ahead of time with relative certainty. Unexpected deviations can, however, have a large impact on option prices.
What does volatility mean for option markets?
Market makers use their assessment of implied volatility to determine the value of option contracts and the bid and offer prices they will show in the market. An option’s implied volatility is dynamic and fluctuates according to changes in the market’s expectation of future price movements in the price of the underlying asset. News events such as earnings announcements could lead to changes in those expectations and result in more or less demand for the option, driving its price up or down regardless of the price movement of the underlying asset.
All else being equal, when implied volatility increases, the value of the option will increase and vice versa. This is because a higher than expected volatility increases the likelihood of the price of the underlying asset further deviating from the strike price, a movement that is positive for the holder of the option. The amount by which the price of put and call options will change in response to a one-point change in implied volatility is expressed by vega, one of the Greek options.
Example
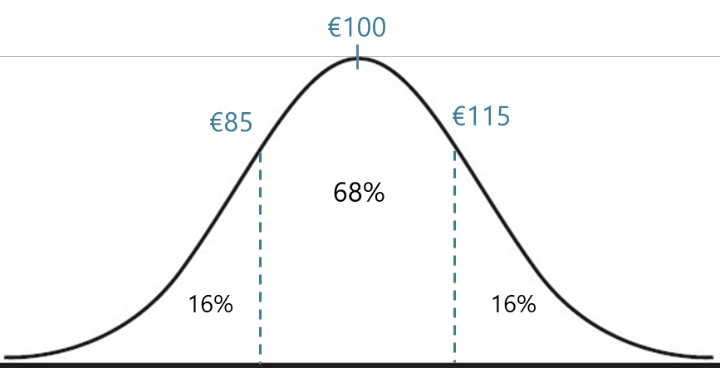
If the shares of Airbus Group are trading at €100 and the implied volatility of an option contract on this share is 15%, then a one standard deviation move over the next 12 months will be plus or minus €100 * 15% = €15.
In theory, it is assumed that the share price follows a normal distribution. This implies that, after one year, the share could end up within one standard deviation of its original price 68% of the time, with a 32% chance the share price will be outside this range.
As such, the implied volatility of 15% means the market’s current expectation is that there is a 68% chance the share price will end up between €85-115 in a year from now.
If the implied volatility were to rise to 20%, there would be a 68% chance the share price would end up between €80-120 and 32% chance it would be outside this range. As the likelihood of the share price deviating further from the strike prices increases, the option contract typically increases in value. If the option’s vega is 0.5, the implied volatility increases from 15% to 20% would result in the option’s price rising by 5 * 0.5 = €2.50.